Speech

Remarks on Optimal Monetary Policy

September 7, 2018

Since the global financial crisis of 2008, a number of stylized facts have triggered intensive research on welfare maximizing, i.e. optimal, monetary policy. In these remarks, I will focus on three of these stylized facts by providing tentative answers to three questions.

• How should the conduct of monetary policy reflect the role of financial conditions?

• Should hysteresis feature in monetary policy?

• Does monetary policy affect r*?

I conclude with some considerations for monetary policy research going forward.

How should the conduct of monetary policy reflect the role of financial conditions?

The first relates to the role of financial conditions in the conduct of monetary policy. The crisis illustrated that macro-financial interactions pose important considerations for the conduct of monetary policy. One particular way of gauging macro-financial linkages is via the pricing of risk, as summarized by measures of financial conditions. I thus ask to what extent financial conditions should feature in the conduct of monetary policy.

To set the stage, I start with a chart from recent work by Adrian, Grinberg, Liang, Malik (2018) who show that the elasticity of downside risk to GDP (as measured by the 5 ^th quantile of GDP) depends significantly positively on financial conditions in the short run, but significantly negatively in the medium run. More specifically, the elasticity of the 5^th GDP quantile with respect to the financial conditions index (FCI) is economically large, highly significant, and positive up to two years in the future (8 quarters) but turns significantly negative in the medium term. The positive coefficient in the short run indicates that looser financial conditions correspond to lower downside risk. The chart also shows the dependence of the median of GDP growth as a function of financial conditions, indicating that loose financial conditions forecast a boost to the central tendency of GDP growth in the short run.

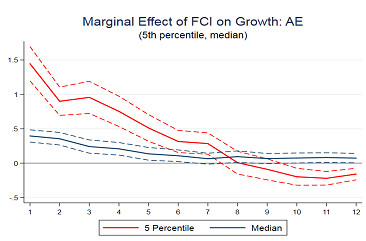
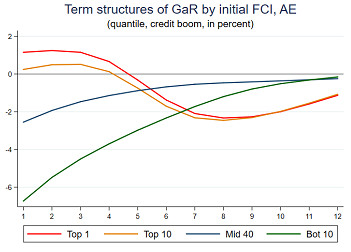
Adrian, Grinberg, Liang, Malik (2018) label the 5^th quantile of GDP growth “GDP at Risk,” or GaR, as it corresponds to the value at risk of future average cumulative GDP growth. The reversal of the elasticity of GaR with respect to FCIs at longer horizons gives rise to an intriguing term structure of GaR over time, as illustrated in the next chart. When financial conditions are loose, measured by the 1^st or 10 ^th percentile of FCIs, the term structure of GaR is downward sloping. Hence, downside risks to GDP growth are low in the short term, but become more sizable in the medium-term. In contrast, when financial conditions are tight, as indicated by the bottom 10^th percentile of FCIs, the term structure of GaR is upward sloping: in the midst of a downturn, downside risks are large, but the medium term future looks less risky. Easier financial conditions in bad times mitigate short term downside risks. Variation in FCIs thus correspond to a macro-financial cycle where easy financial conditions indicate increasing downside risks into the future, while tight financial conditions indicate declining downside risks into the future.

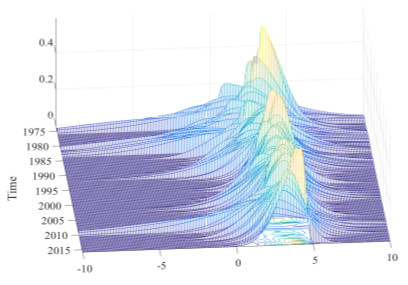
These interactions between FCIs and downside risks to GDP growth give rise to a highly skewed conditional GDP distribution. The next figure, from Adrian, Boyarchenko, Giannone (2018) shows that the conditional mean and the conditional volatility of GDP growth one year ahead tend to be negatively correlated. When financial conditions are easy, conditional volatility is low, and expected growth is high. An adverse shock to financial conditions is associated with an increase in volatility, and a decline in expected growth, and hence the GDP growth distribution tends to be negatively skewed.

These stylized facts of the dynamic interaction of the GDP growth distribution and the level of financial conditions can be parsimoniously represented in a standard New Keynesian model of the macroeconomy that incorporates endogenous risk, as studied by Adrian and Duarte (2018) . The IS curve features endogenous volatility which itself is a function of expected growth. Hence risk is endogenous, and the negative correlation between the conditional mean and the conditional variance of the GDP distribution is hard-wired in the model. The Phillips curve is standard. Adrian and Duarte (2018) study optimal monetary policy in such a microfounded framework.

The policy maker is assumed to feature a standard quadratic loss function with the output gap and inflation deviation from target as inputs. The optimal monetary policy rule is derived in closed form by Adrian and Duarte (2018) and depends on the level of financial conditions, in addition to the output gap and inflation. In simulations, Adrian and Duarte (2018) show that the steady state distribution of output using the optimal monetary policy rule features less negative skewness and lower volatility of GDP when compared to a standard Taylor rule. Intuitively, monetary policy impacts not only the consumption-savings decision, but also the riskiness of GDP, and hence a policy maker optimally balances the impact of monetary policy on expected growth and on downside risk. This observation is indeed very related to the practice of many central banks that explicitly take the balance of risk into account when setting monetary policy decisions. The emphasize of financial conditions to impact not only expected growth and inflation, but also the downside risks to growth, is what Adrian and Duarte (2018) emphasize relative to the current practice. Of course, the degree to which financial conditions weigh in the optimal policy rule depends on the intertemporal preferences of the policy maker, and on the relative weight that the policy maker puts on the output gap. In preliminary calibrations, Adrian and Duarte (2018) uncover a policy rule that leans slightly against the buildup of risk when the economy is close to potential (in comparison to a standard Taylor rule), and that aggressively loosens when the economy is contracting.

Should hysteresis feature in monetary policy?

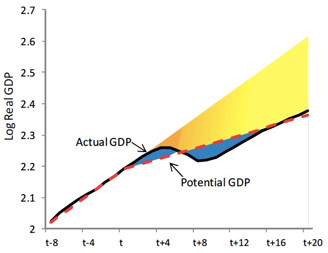
The second question that I consider is related to the pervasive observation of hysteresis in negative shocks to GDP growth. Over time and across countries, deep recessions tend to be followed by persistently low growth for an extended period of time, leading to a revision of trend productivity growth, as documented by Carrera and Saxena ( 2008, 2017 ). The next figure, from Blanchard, Cerutti, and Summers (2015) , illustrates this behavior: Potential GDP tends to fall in a persistent manner when recessions occur. This finding is at odds with the traditional distinction between trend and cycle, where monetary policy is concerning itself only with cyclical variation in output, while variation in potential GDP is considered to be associated with supply side movements.

Benigno and Fornaro (2018) show that a standard New Keynesian model with endogenous growth can generate such hysteresis. The model features an efficient equilibrium with a high level of output and high growth, and an inefficient equilibrium with low output and low growth. This multiplicity of equilibria is illustrated in the next chart.

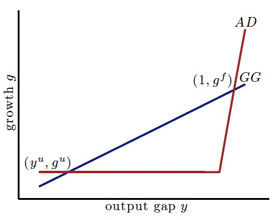
Garga and Singh (2018) study optimal monetary policy within such New Keynesian models with endogenous growth. These authors show that optimal monetary policy is an inflation targeting rule that conditions on a hysteresis gap, in addition to the more traditional output gap and inflation. The hysteresis gap relates to the distance of current trend growth from the efficient trend growth and is driven by the level of endogenous productivity. Targeting hysteresis arises both under commitment and under discretion conditional on supply and demand shocks. The existence of a zero lower bound complicates monetary policy, worsening the costs of hysteresis. Of course, these are tentative conclusions that need to be studied further.

Does monetary policy affect r*?

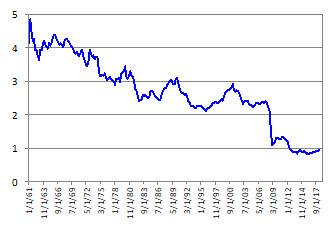
The natural interest rate r* is generally defined as the real short-term interest rate that would prevail if inflation were at its target and employment were full. Estimates of r* have fallen in recent decades. The next figure shows a measure of global r* by averaging estimated r* from Holston, Laubach, Williams (2017) across the US, UK, Euro Area, and Japan. This gauge of global r* fell from over 4% in the early 1960s to less than 1% in the most recent decade.

While r* is the right metric of a neutral stance of monetary policy when price stickiness is the only friction, in economies with additional frictions, such as the financial frictions discussed above, the notion of an efficient r*, or r^e, is the right benchmark for optimal monetary policy. Intuitively, monetary policy sets a path of interest rates that optimally trades off frictions to try to achieve the efficient equilibrium. When the policy maker manages to achieve that equilibrium, real interest rates equal r^e.

In general, r^e is impacted by supply factors such as demographics or trend productivity growth. Financial frictions that interact with the supply side of the economy might also affect r ^e. For example, the endogenous pricing of risk in the economy of Adrian and Duarte (2018) might impact capital accumulation in productive or housing capital, thus impacting r^e in an extended model. The impact of such interactions between the supply side and the endogenous buildup of risk on the evolution of r^e has not yet been worked out in the literature, to my knowledge.

Conceptually, the definition of r^e does not depend on monetary policy, as the efficient real rate is computed taking various frictions into account. When policy makers do not have enough instruments to address all distortions in the economy, they use the available ones to weigh among distortions. Those frictions are driving a wedge between the actual and the efficient output, and between inflation and the target, and hence monetary policy is used to get these state variables as close as possible to the efficient levels. In comparison, the computation of r*, as shown above based on Holston, Laubach, Williams (2017), does not take any financial frictions into account, relying instead on the assumption that sticky prices are the sole friction in the economy.

Going Forward

The macro-financial literature since the crisis of 2008 has brought to light that three stylized facts should be considered by monetary policy makers: 1) Financial frictions matter for the distribution of future GDP growth; 2) Recessions are associated with hysteresis of trend growth; and 3) The natural rate of interest has fallen markedly. The monetary policy literature has analyzed each of these stylized facts in isolation, but has not yet considered them jointly. It seems particularly promising to introduce financial frictions into New Keynesian settings with endogenous growth, thus asking to what extent the endogenous evolution of macroeconomic risk interacts with hysteresis. Such a model might in turn lead to strong variation in the efficient rate of interest, with associated implications for the conduct of monetary policy.

Borio, Disyatat, Rungcharoenkitkul (2018) study optimal monetary policy in a setting where a leverage cycle is a friction in addition to sticky prices. They argue that the leverage cycle leads to a novel estimate of the natural rate, which takes financial cycle imbalances into account over and above cycles in product markets. This works goes some direction toward modeling hysteresis and financial frictions jointly, but more needs to be done to draw robust conclusions for optimal monetary policy.

Literature

Adrian, Tobias, Nina Boyarchenko, and Domenico Giannone (2018), “Vulnerable Growth” American Economic Review, forthcoming.

Adrian, Tobias, and Fernando Duarte (2017), “Financial Vulnerability and Monetary Policy” Federal Reserve Bank of New York Staff Reports 804.

Adrian, Tobias, Federico Grinberg, Nellie Liang, Sheheryar Malik (2018), “The Term Structure of Growth at Risk,” IMF Working Paper.

Benigno, Gianluca and Luca Fornaro (2018), “Stagnation Traps,” Review of Economic Studies 85(3), pp. 1425-1470.

Blanchard, Olivier, Eugenio Cerutti, and Larry Summers (2015), “Inflation and Activity: Two Explorations and their Monetary Policy Implications,” IMF Working Paper 15/230.

Borio, Claudio, Piti Disyatat, Phurichai Rungcharoenkitkul (2018), “What Anchors the Natural Rate of Interest?” BIS Working Paper.

Carrera, Valerie and Sweta Saxena (2008) “Growth Dynamics: the Myth of Economic Recovery,” American Economic Review 98(1), 439-57.

Carrera, Valerie and Sweta Saxena (2017) “Booms, Crises, and Recoveries: A New Paradigm of the Business Cycle and its Policy Implications,” IMF Working Paper 17/250.

Garga, Vaishali and Sanjay R. Singh (2018), “Output Hysteresis and Optimal Monetary Policy,” Brown University Working Paper.

Holston, Kathryn, Thomas Laubach, John C. Williams (2017), “Measuring the Natural Rate of Interest: International Trends and Determinants,” Journal of International Economics 108, pp. 59-75.