Dornbusch's Overshooting Model After Twenty-Five Years, The Mundell-Fleming Lecture by Kenneth Rogoff, Economic Counselor and Director of the IMF Research Department
November 29, 2001
Mundell-Fleming Lecture
Kenneth Rogoff1
Economic Counselor and Director of the IMF Research Department
November 30, 2001 (revised January 22, 2002)
I. Introduction
It is a great honor to pay tribute here to one of the most influential papers written in the field of International Economics since World War II. Rudiger Dornbusch's masterpiece, "Expectations and Exchange Rate Dynamics" was published twenty-five years ago in the Journal of Political Economy, in 1976. The "overshooting" paper-as everyone calls it-marks the birth of modern international macroeconomics. There is little question that Dornbusch's rational expectations reformulation of the Mundell-Fleming model extended the latter's life for another twenty-five years, keeping it in the forefront of practical policy analysis.
This lecture is divided into three parts. First, I will try to convey to the reader a sense of why "Expectations and Exchange Rate Dynamics" has been so influential. My goal here is not so much to offer a comprehensive literature survey, though of course there has to be some of that. Rather, I hope the reader will gain an appreciation of the paper's enormous stature in the field and why so much excitement has always surrounded it. To that end, I have also included some material on life in Dornbusch's MIT classroom. The second part of the lecture is a more detached discussion of the empirical evidence for and against the model, and a thumbnail sketch of the model itself. The final section touches on competing notions of overshooting.
II. The Overshooting Model in Perspective
One of the first words that comes to mind in describing Dornbusch's overshooting paper is "elegant". Policy economists are understandably cynical about academics' preoccupation with theoretical elegance. But Dornbusch's work is a perfect illustration of why the search for abstract beauty can sometimes yield a large practical payoff. It is precisely the beauty and clarity of Dornbusch's analysis that has made it so flexible and useful. Like great literature, Dornbusch (1976) can be appreciated at many levels. Policymakers can appreciate its insights without reference to extensive mathematics; graduate students and advanced researchers found within it a rich lode of subtleties.
A second word to describe the work is "path breaking". I will offer some quantitative evidence later, but suffice to say here that literally scores of Ph.D. theses (including my own) have built upon Dornbusch (1976). It is not hyperbole to say that Dornbusch's new view of floating exchange rates reinvigorated a field that was on its way to becoming moribund, using only dated, discredited models and methods. Dornbusch (1976) inspired fresh thinking and brought in fresh faces into the field. In preparing this lecture, I re-read Maurice Obstfeld's superb inaugural Mundell-Fleming lecture from last year (IMF Staff Papers, Vol. 47, 2001). Obstfeld's paper spans the whole modern history of international macroeconomics, from Meade to "New Open Economy Macroeconomics", but the main emphasis is on Bob Mundell's papers. I, and perhaps many other readers, found Obstfeld's discussion enlightening in part because we do not have the same intimate knowledge of Mundell's papers that we do of Dornbusch (1976). Mundell's profoundly original ideas are, of course, at the core of many things we do in modern international finance, and he was the teacher of many important figures in the field including Michael Mussa, Jacob Frenkel, and Rudiger Dornbusch. Mundell is a creative giant who was thinking about a single currency in Europe back when intergalactic trade seemed like a more realistic topic for research. But the methods and models in Mundell's papers are now badly dated, and are not always easy to digest for today's reader (even if at the time they seemed a picture of clarity compared to the existing state of the art, Meade (1951)). One of the remarkable features of Dornbusch's paper is that today's graduate students can still easily read it in the original and, as I will document, many still do.
The reader should understand that as novel as the overshooting model was, Dornbusch was hardly writing in a vacuum. Jo Anna Gray (1976), Stanley Fischer (1977), and Ned Phelps and John Taylor (1977) were all working on closed economy sticky-price rational expectations models at around the same time. Stanley Black (1973) had already introduced rational expectations to international macroeconomics. Dornbusch's Chicago classmate Michael Mussa (my predecessor as Economic Counsellor at the Fund) was also working actively in the area in the time, though he delayed publication of his main piece on the topic until Mussa (1982). There were others who were fishing in the same waters as Dornbusch at around the same time, (e.g., Hans Genberg and Henryk Kierzkowski, 1979). But the elegance and clarity of Dornbusch's model, and its obvious and immediate policy relevance, puts his paper in a separate class from the other international macroeconomics papers of its time.
A. Still a Useful Policy Tool A word about New Open Economy Macroeconomics, which Obstfeld surveyed last year; certainly this literature has come to dominate the academic literature on international macroeconomic policy.2 Superficially, of course, most of the newer generation models appear quite different from Dornbusch's model, not least because they introduce rigorous microfoundations for consumer and investor behavior. At the same time, however, they can be viewed as direct descendants. Formally, New Open Economy Macroeconomics attempts to marry the empirical sensibility of the sticky-price Dornbusch model with the elegant but unrealistic "intertemporal approach to the current account".3 But even with the inevitable onslaught of more modern approaches, the Dornbusch model is still very much alive today on its own, precisely because it is so clear, simple and elegant. Let's be honest. If one is in a pinch and needs a quick response to a question about how monetary policy might affect the exchange rate, most of us will still want to check any answer against Dornbusch's model. Dornbusch's variant of the Mundell-Fleming paper is not just about overshooting. The general approach has been applied to a host of different problems, including the "Dutch disease," the choice of exchange rate regime, commodity price volatility, and the analysis of disinflation in developing countries. It is a framework for thinking about international monetary policy, not simply a model for understanding exchange rates. But what sold the paper to policymakers, what still sells the paper to graduate students, is overshooting. One has to realize that at the time Dornbusch was writing, the world had just made the transition from fixed to flexible exchange rates, and no one really understood what was going on. Contrary to Friedman's (1953) rosy depiction of life under floating, exchange rate changes did not turn out to smoothly mirror international inflation differentials. Instead, they were an order of magnitude more volatile, far more volatile than most experts had guessed they would be. Along comes Dornbusch who lays out an incredibly simple theory that showed how, with sticky prices, instability in monetary policy-and monetary policy was particularly unstable during the mid-1970s-could be the culprit, and to a far greater degree than anyone had imagined. Dornbusch's explanation shocked and delighted researchers because he showed how overshooting did not necessarily grow out of myopia or herd behavior in markets. Rather, exchange rate volatility was needed to temporarily equilibrate the system in response to monetary shocks, because underlying national prices adjust so slowly. It was this idea that took the paper from being a mere "A" to an "A++". As we shall see, Dornbusch's conjecture about why exchange rates overshoot has proven of relatively limited value empirically, although a plausible case can be made that it captures the effects of major turning points in monetary policy. But the true strength of the model lies in that it highlights how, in today's modern economies, one needs to think about the interaction of sluggishly adjusting goods markets and hyperactive asset markets. This broader insight certainly still lies at the core of modern thinking about exchange rates, even if the details of our models today differ quite a bit. Paul Samuelson once remarked that there are very few ideas in economics that are both (a) true and (b), not obvious. Dornbusch's overshooting paper is certainly one of those rare ideas. Now, of course, unless one is steeped in recent economic theory, little of what appears in today's professional economics journals will seem obvious. However, that is only because it takes constant training and retooling to be able to follow the assumptions in the latest papers. Once you can understand the assumptions, what follows is usually not so surprising. But this is certainly not the case with the "overshooting" result, as I will now briefly illustrate. B. Overshooting: The Basic Idea Since this lecture is aimed at a broad audience, it is not my intention to invoke too many mathematical formulas, though there will be a few. A small number of equations is necessary if only to impress upon the reader how simple the concept really is. The reader can easily skip over them. Two relationships lie at the heart of the overshooting result. The first, equation (1) below, is the "uncovered interest parity" condition. It says that the home interest rate on bonds, i, must equal the foreign interest rate i*, plus the expected rate of depreciation of the exchange rate, Et (et+1 - et), where e is the logarithm of the exchange rate (home currency price of foreign currency)4, and Et denotes market expectations based on time t information. That is, if home and foreign bonds are perfect substitutes, and international capital is fully mobile, the two bonds can only pay different interest rates if agents expect there will be compensating movement in the exchange rate. Throughout, we will assume that the home country is small in world capital markets, so that we may take the foreign interest rate i* as exogenous.5 Uncovered interest rate parity
Indeed, Dornbusch assumed "perfect foresight" in his model-essentially that there was no uncertainty-since techniques for incorporating uncertainty were not yet fully developed at the time of his writing; the distinction between perfect foresight and rational expectations is not consequential for our analysis here. Does uncovered interest parity really hold in practice? Many a paper has been written on the topic, and the short answer is no, not exactly. Several recent attempts to reconcile exchange rate theory and data turn on generalizing this equation, though it remains to proven how fruitful this approach will be.6 The second core equation of the Dornbusch model is the money demand equation Money demand
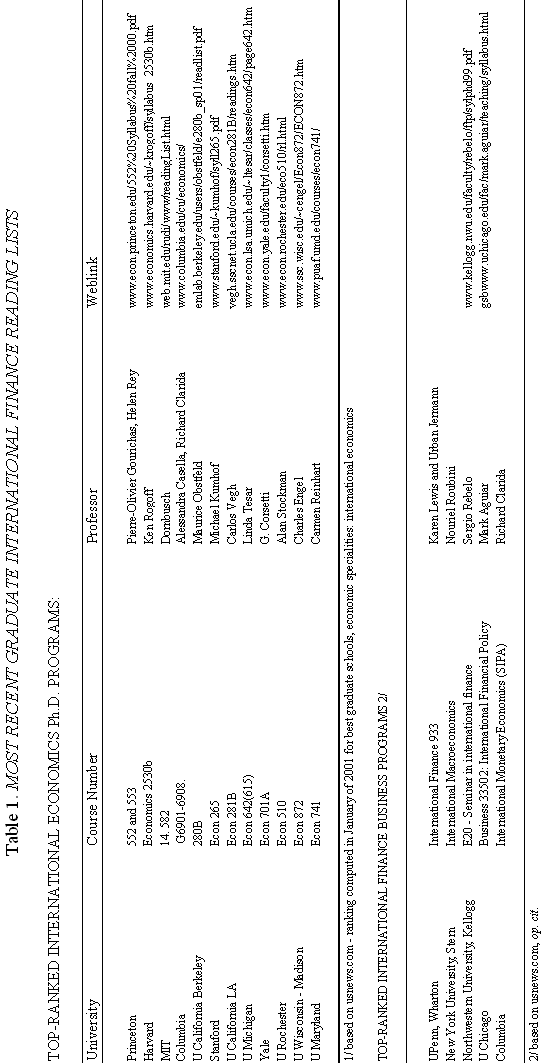
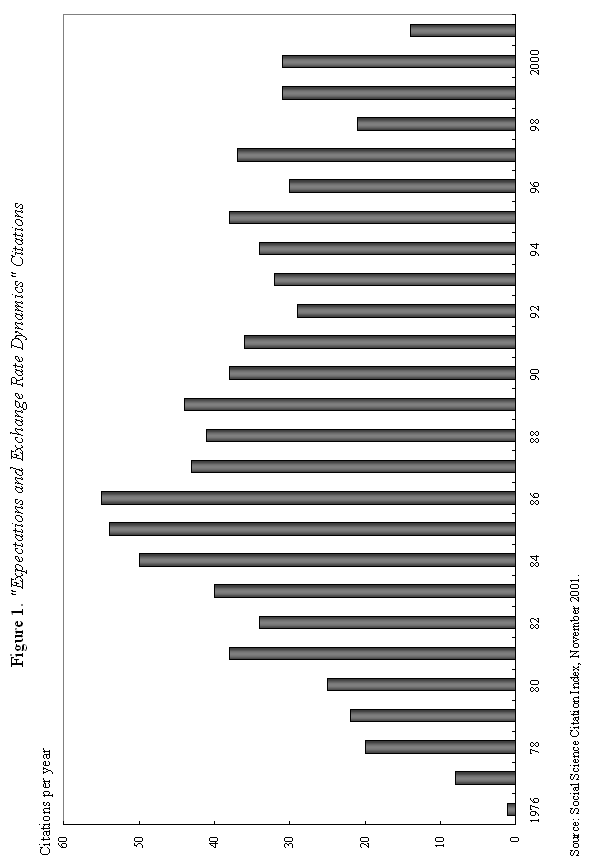
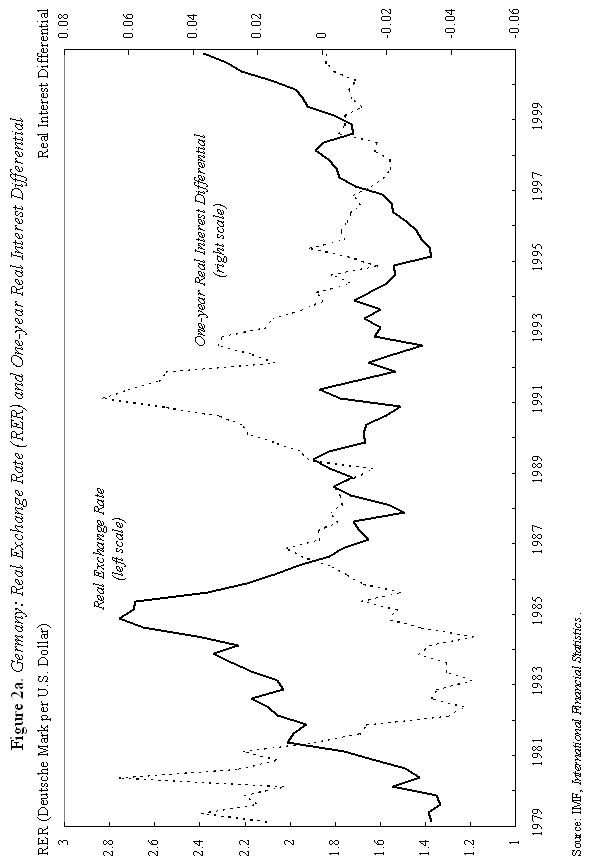
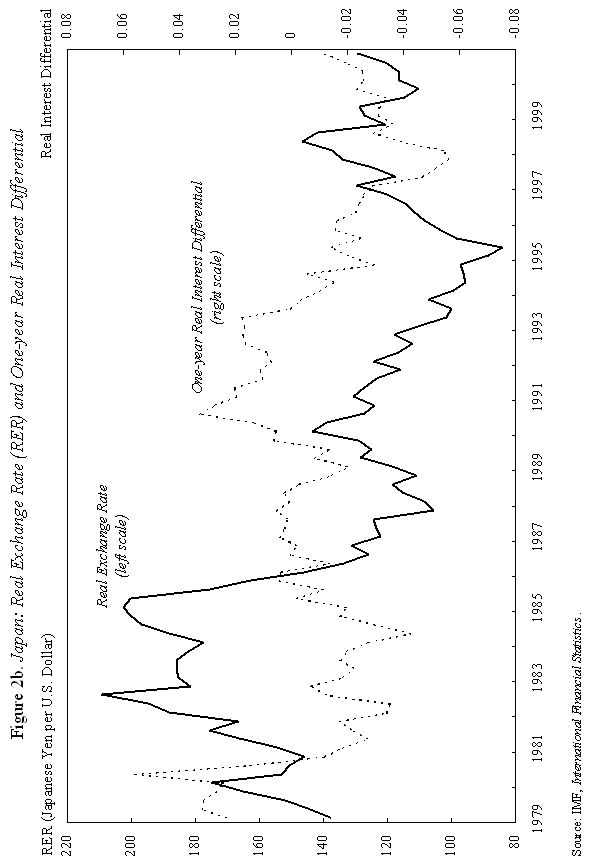
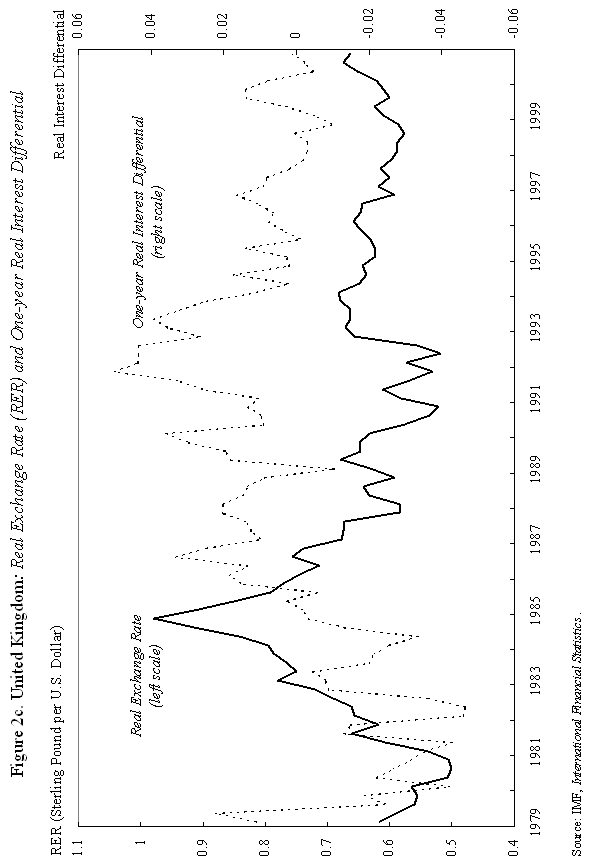
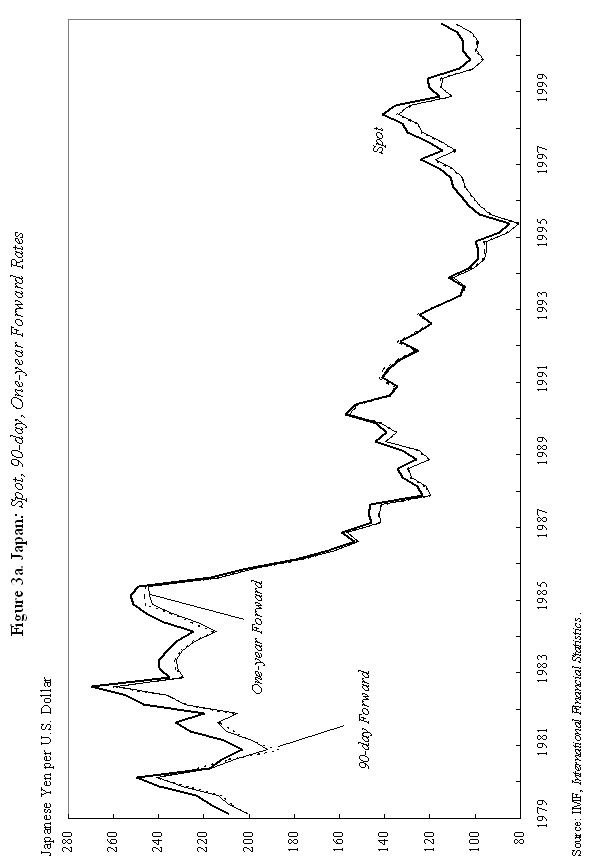
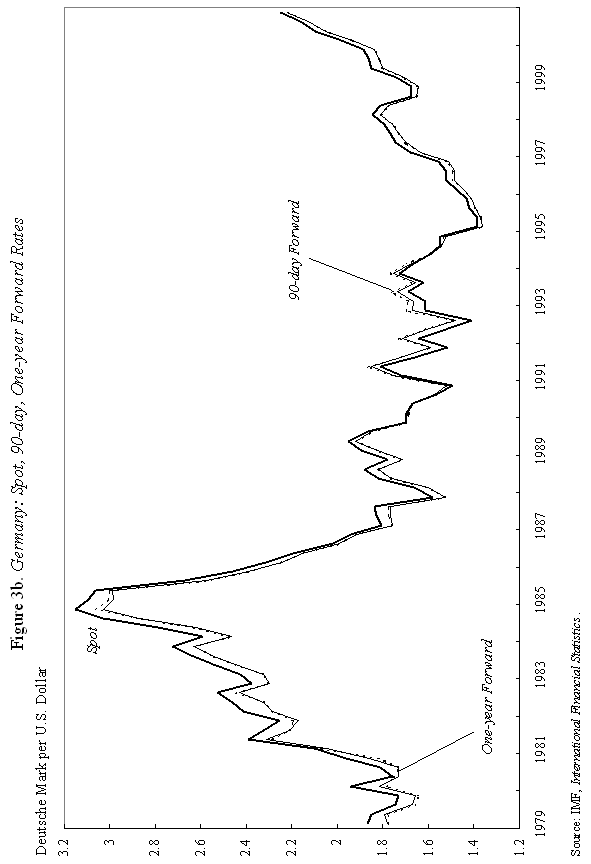
where m is the money supply, p is the domestic price level, and y is domestic output, all in logarithms; So how does "overshooting" work? It can all be captured by combining equations (1) and (2) with a few simple assumptions. First, assume that the domestic price level p does not move instantaneously in response to unanticipated monetary disturbances, but adjusts only slowly over time. We shall say more about this assumption shortly, but it is certainly empirically realistic. As Mussa (1986) so convincingly demonstrated, domestic price levels generally have the cardiogram of a rock compared to floating exchange rates, at least in countries with trend inflation below, say, 100-200 percent per annum. Second, assume that output y is exogenous (what really matters is that it, too, moves sluggishly in response to monetary shocks). Third, we will assume that money is neutral in the long run, so that a permanent rise in m leads a proportionate rise in e and p, in the long run.7 Now suppose, following Dornbusch's famous thought experiment, that there is an unanticipated permanent increase in the money supply m. If the nominal money supply rises but the price level is temporarily fixed, then the supply of real balances m-p must rise as well. To equilibrate the system, the demand for real balances must rise. Since output y is assumed fixed in the short run, the only way that the demand for real balances can go up is if the interest rate i on domestic currency bonds falls. According to equation (1), it is possible for i to fall if and only if, over the future life of the bond contract, the home currency is expected to appreciate. But how is this possible if we know that the long run impact of the money supply shock must be a proportionate depreciation in the exchange rate? Dornbusch's brilliant answer is that the initial depreciation of the exchange rate must, on impact, be larger than the long-run depreciation. This initial excess depreciation leaves room for the ensuing appreciation needed to simultaneously clear the bond and money markets. The exchange rate must overshoot. Note that this whole result is driven by the assumed rigidity of domestic prices p. Otherwise, as the reader may check, e, p, and m would all move proportionately on impact, and there would be no overshooting. Put differently, money is neutral here if all nominal quantities, including the price level, are fully flexible. Of course, I have left out a lot of details, and we need to check them to make sure that this story is complete and hangs together. We will do it later. Fundamentally, however, the power and generality of the overshooting idea derives precisely from the fact that it can be cooked with so few ingredients. The only equations we need are (1) and (2), and therefore the result is going to obtain across a broad class of models that incorporate sticky prices. Now underlying Dornbusch's disarmingly simple result lies some truly radical thinking. At the time Rudi was working on his paper, the concept of sticky prices was under severe attack. In his elegant formalization of the Phelps islands model, Lucas (1973) suggested that one could understand the real effects of monetary policy without any appeal to Keynesian nominal rigidities, and by 1975, Lucas had many influential followers in Sargent, Barro and others. The Chicago-Minnesota School maintained that sticky prices were nonsense and continued to advance this view for at least another fifteen years. It was the dominant view in academic macroeconomics. Certainly, there was a long period in which the assumption of sticky prices was a recipe for instant rejection at many leading journals. Despite the religious conviction among macroeconomic theorists that prices cannot be sticky, the Dornbusch model remained compelling to most practical international macroeconomists. This divergence of views led to a long rift between macroeconomics and much of mainstream international finance. Of course, today, the pendulum has swung back entirely, and there is a broad consensus across schools of thought that some form of price rigidity is absolutely necessary to explain real-world data, in either closed or open economies. The new view can be found in many places, but certainly in the closed economy work of authors such as Rotemberg and Woodford (1997), Woodford (2002), and of course in New Open Economy Macroeconomics. The Phelps-Lucas islands paradigm for monetary policy is, for now, a footnote (albeit a very clever one) in the history of monetary theory. There are more than a few of us in my generation of international economists who still bear the scars of not being able to publish sticky-price papers during the years of new neoclassical repression. I still remember a mid-1980s breakfast with a talented young macroeconomic theorist from Barcelona, who was of the Chicago-Minnesota school. He was a firm believer in the flexible-price Lucas islands model, and spent much of the meal ranting and raving about the inadequacies of the Dornbusch model: "What garbage! Who still writes down models with sticky prices and wages! There are no microfoundations. Why do international economists think that such a model could have any practical relevance? It's just ridiculous!" Eventually the conversation turns and I ask, "So, how are you doing in recruiting? Your university has made a lot of changes." The theorist responds without hesitation: "Oh, it's very hard for Spanish universities to recruit from the rest of the world right now. With the recent depreciation of the exchange rate, our salaries (which remained fixed in nominal terms) have become totally uncompetitive." Such was life. C. Cite Counts and Course Reading Lists Since we are here to focus on the innate beauty of the Dornbusch model, it is perhaps crass to list citation counts and other quantitative measures of influence. In principle, however, economics is a quantitative science, so please forgive me for doing so. For the period 1976-2001, the social science citation index (of major economics journals) shows 917 published articles citing Dornbusch (1976). This includes 42 separate articles in International Monetary Fund Staff Papers. Roughly 40 percent of the issues of Staff Papers published between 1977 and 2001 included at least one article citing the Dornbusch model; the Fund should have given him a column. This is influence! Oh, yes, as an afterthought, I should note that Dornbusch's article has also been cited in 40 different articles in the American Economic Review and the Journal of Political Economy, the leading professional economics journals. To put these numbers in perspective, the reader should understand that for the typical middle-aged scholar at a top-five American university, 500 citations lifetime is not a bad count for all of one's articles, much less a single one. Figure 1-which at first glance looks like the hill program on a "stairmaster" exercise machine-gives the time trajectory of citations for Dornbusch's article. The article's peak citation years were 1984-86, when it received over 50 citations per year. Not bad for an article ten years after being written. Even towards the end of the nineties, Dornbusch (1976) was still getting over 25 citations per year. And remember, these figures only includes journal articles, not books and conferences.8 Another measure of influence is inclusion on reading lists for advanced graduate courses in international finance. In 1990, Alan Deardorf performed an informal survey of international finance reading lists at leading graduate programs. To his surprise, only one article was listed on more than half of the reading lists, and this particular article was listed on every single one. Guess which article it was? Today, since virtually every course-reading list is posted on the Web, conducting such a survey is much easier. Table 1 lists the top-ranked international economics Ph.D. programs according to U.S. News and World Report. Also listed are the top ranking international finance business programs. One finds that Dornbusch's article is listed on virtually every course reading list, with the only exception being a few cases where only Chapter 9 of Obstfeld and Rogoff (1996)-which contains an exposition of the Dornbusch model-is listed. Clearly the Dornbusch article's influence in teaching is still alive and well as we mark its twenty-fifth anniversary. The broad concept of overshooting has taken on a life far beyond the academic sphere. One can find the idea of exchange rate overshooting regularly invoked in the pages of the financial press and in the speeches of major policy leaders. During 1999-2000, the Economist magazine contained 14 articles including the terms "overshooting" and "exchange rates." During 2001, the Financial Times had eleven references to overshooting. In recent months, both Federal Reserve Chairman Alan Greenspan (June 2001) and Bank of France President Jean-Claude Trichet (May 2001) have discussed overshooting in speeches, and one can find countless more references by other world financial leaders, not least in developing countries. This, too, is influence. D. Learning from the Master: Life at MIT in Dornbusch's International Finance Course Before proceeding to more analytic material, it is perhaps helpful to say a bit about how this author first learned the Dornbusch model. This will also give the reader a bit of the flavor of the period. I sat in on Rudi's course in the spring of 1977. ("Spring," anyway, is the euphemism that MIT uses for the semester that starts in February.) Dornbusch's classes during the three years 1976-78 included many MIT students who went on to become luminaries in the field. A short list would include Paul Krugman, Jeffrey Frankel and Maurice Obstfeld, but there are literally scores of others who went on to distinguished academic careers. There were several future finance ministers and heads of central banks as well. My 1977 class happened to include the brilliant and charming Eliana Cardoso, whom Dornbusch later married. Sitting beside the MIT students, there were also many Ph.D. students from Harvard, who braved the Cambridge winter to study at the master's knee. These included Larry Summers and Jeffrey Sachs. Rudi has what can only be described as a confrontational style of teaching, challenging his class with a mix of incredibly difficult questions. To make things even more challenging, his class typically meets very early in the morning, far earlier than the typical graduate student is accustomed to rising. To put himself at further advantage, as if he needed, it, Dornbusch has a habit of writing down graphs without labeling the axes, a technique he learned from his own teacher, Robert Mundell. I guess if I had really understood what was going on back then, it would have been easy to follow which way the curves were supposed to shift. More often than not, however, I had to go back after class and recheck the article he was supposed to be teaching-if it had been written yet. At least I was not alone in being unable to answer so many of the questions. Having witnessed Rudi engage the likes of young Larry Summers, Paul Krugman and Jeffrey Sachs, I would venture that Dornbusch's international finance course at MIT is the answer to the trivia question "When was the last time these guys were completely humiliated in public?" The day when Dornbusch presented his 1976 overshooting paper was different. All the graphs were labeled that day and he seemed to have organized notes, not that he drew on them much. The excitement in the room was palpable, as the logic behind overshooting unfolded. You could see in the students' faces that something special was happening. The ideas in Dornbusch (1976) have inspired countless students to choose international economics as a field. This author is certainly among them. III. Theory and Empirics A. The Data We have come to praise the overshooting model, not to bury it, but it is time for a few hard facts about the data. Now, if there is a consensus result in the empirical literature, it has to be that nothing, but nothing, can systematically explain exchange rates between major currencies with flexible exchange rates. This point was first stated in such radical form by Meese and Rogoff (1983), and it very much still stands today.9 The basic problem with the Dornbusch model is that whereas it seems to capture major turning points in monetary policy quite well (e.g., the Volcker deflation of the early 1980s in the United States and the Thatcher deflation of the late 1970s in Britain), the model does not seem to capture all the other big exchange rate swings that regularly take place. Formally testing the Dornbusch model is easier said than done. To take the model to the data, one needs to resolve many issues. These include, not least, how to allow for more general types of monetary disturbances, for the endogeneity of the money supply and interest rates, for real shocks, etc. Perhaps the most robust empirical prediction of the model is Jeffrey Frankel's (1979) observation that, under a reasonably general set of assumptions-which include that monetary shocks must be a predominant source of disturbances-a generalized Dornbusch model predicts that the real exchange rate and the real interest differential will be positively correlated. That is, high real interest rates will bid up the real exchange rate. Frankel's generalization is an important one since if a rise in the money supply signals high future inflation, it will have very different effects on long-term nominal interest rates than if the rise in the money supply is viewed as a temporary easing. Focusing on real interest rates turns out to finesse this problem. Figure 2a gives a graph of the US dollar rate versus the German mark. (For future generations reading this lecture, I will note that the mark was Germany's currency before the euro.) The solid line gives the real exchange rate, and the dashed line is the one-year real interest differential.10 A rise in the real exchange rate represents a depreciation of the mark, and a rise in the real interest differential represents a rise in German real interest rates relative to those prevailing in the United States. As one can see, the model does seem to say something about major turning points, though we will not press to see if it robustly passes regression tests.11 Figure 2b for the Japanese yen versus the dollar tells a similar story. Even this tenuous relationship between real exchange rates and the real interest differential we see in Figures 2a and 2b is not universal. Figure 2c gives the UK pound against the dollar; the relationship between the two series, if there is one, hardly jumps off the page. Another piece of evidence comes from looking at the co-movements of forward and spot exchange rates, as Robert Flood highlighted in his 1981 Carnegie-Rochester paper. Flood's basic point is that, in most cases, the overshooting model predicts that forward rates and spot rates will not, in general, move one for one. The exact comovement depends on the nature of the shock (real versus nominal, temporary versus permanent) and on the horizon of the forward rate. In Dornbusch's thought experiment of a one-time unanticipated change in the level of the money supply, the spot rate should move by more than the forward rate at any horizon. This excess movement is precisely the overshooting. Figure 3a graphs movements of the spot rate together with 90-day and one-year forward rates for the yen/dollar exchange rate. Movements in the three series are almost indistinguishable. The same observation holds for Figure 3b, which gives the mark/dollar exchange rate. Now, if we were to magnify these graphs, a bit more daylight would appear between the curves. Indeed, as Table 2 illustrates, forward rate volatility is slightly lower than spot rate volatility over the sample period. Though it would be straightforward, I do not actually test to see whether the differences are statistically significant. The overarching point is that the differences are small. Figures 3 may not constitute decisive evidence against overshooting, but nor does it give strong support to the concept.12 Does the empirical failure of the Mundell-Fleming-Dornbusch model mean that we have to reject it as a useful tool for policy analysis? Not at all. First, although the overshooting concept beautifully illustrates the inner workings of the model, the broader usefulness of the Mundell-Fleming-Dornbusch model goes well beyond the overshooting prediction. It is a generalized framework for thinking about international macroeconomic policy. Second, as well shall see in the next section, the model does not necessarily predict overshooting when output is endogenous. Third, in newer models consumption typically appears in place of output in the money demand equations; this change also tilts the balance away from overshooting. Now, I would be the last to claim that the generalized failure of structural exchange rate models, as found in the post Meese-Rogoff (1983) literature, should not be taken seriously, even though there has been some progress here in the recent literature towards resolving these puzzles.13 Rather, the apparent ability of the Dornbusch model to describe the trajectory of the exchange rate after major shifts in monetary policy is more than enough reason for us to press ahead and look more deeply at its underlying theoretical structure. Regardless, of course, Dornbusch's model was an important precursor to today's exchange rate literature. B. The Model At this point, it would be helpful to venture a bit more deeply into the inner workings of the model. Doing so allows us to further explore its ideas and contributions. If the reader would like to finesee this technical material, she may skip to the next section. We already have the first two equations of the model, equations (1) and (2) above, the uncovered interest parity and the money demand equations. The only nuance is that since the Dornbusch model abstracts from uncertainty (except for an initial one-time shock), one can replace the expected value of the rate of change of the exchange rate, Et (et+1 - et), with its actual value, et+1 - et, in equation (1). One of the central elements of Dornbusch's model, which I have skipped over until now, is that it was among the first papers to introduce rational expectations into international macroeconomics.14 Imposing "rational expectations" here implies that private agents must form exchange rate expectations in a way that is consistent with the model itself. In this sense, rational expectations is a way of imposing overall consistency on one's theoretical analysis. The idea has enormous appeal, but took some time to penetrate the economics profession, not least because few economists were familiar with the now standard techniques needed to implement it. In fact, Dornbusch himself clearly learned the technique of rational expectations over the course of his research on sticky-price exchange rate models. He had already published a closely-related paper in the Journal of International Economics (Dornbusch, 1976b), which contains the core of the overshooting model, but did not incorporate rational expectations. The assumption of rational expectations made the model far more intriguing. Policymakers found it sobering to learn that in a world of fast-clearing asset markets and slow-clearing goods markets, exchange rate overshooting might be a rational response to monetary shocks. Equation (3) below posits that aggregate demand depends on the real exchange rate. Dornbusch (1976b) has a bit more complicated specification in which the real interest rate also matters, but this nuance is unimportant for our purposes. The main feature of the model is the Keynesian assumption that the price of domestic goods cannot adjust immediately to clear the goods market. As a consequence, aggregate demand yd can temporarily deviate from its full-employment level, Aggregate demand
where The final element of Dornbusch's model is the price adjustment equation. That prices must eventually adjust to a monetary shock may seem obvious to us today. Dornbusch's treatment, however, was in stark contrast to the canonical Mundell-Fleming model of his era, in which the domestic price level was typically assumed fixed, and any dynamics depended on wealth accumulation.15 Rather than use Dornbusch's exact formulation, we will use a price adjustment mechanism proposed by Mussa (1982), which has many virtues. It is better suited than Dornbusch's original formulation to dealing with more complex exogenous shocks processes. At the same time, it turns out to greatly simplify analysis of the system's dynamics.16
where To solve the model, it is helpful to reduce the above equations to a set of two simultaneous difference equations. If we define the real exchange rate as Real exchange rate
and normalize the log of the fixed foreign price level p* to zero, then the price adjustment equation (4) can be written as Real exchange rate adjustment
Note that equation (5) happens to be of the same form as the standard empirical equation one sees estimated in the large literature aimed at calculating the speed at which deviations from purchasing power parity die out.18 The second equation of the dynamic system can basically be derived from the money demand and uncovered interest parity equations, making use of the definition of the real exchange rate q. It is given by Nominal exchange rate adjustment
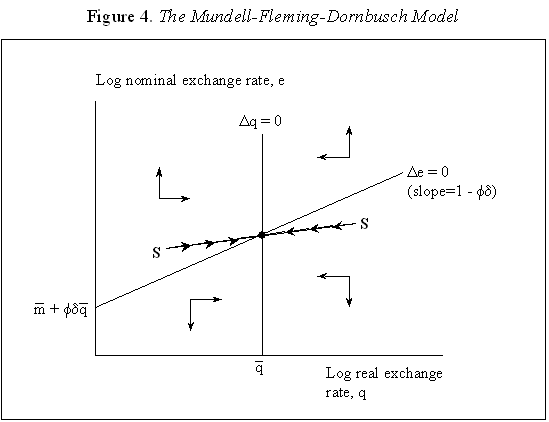
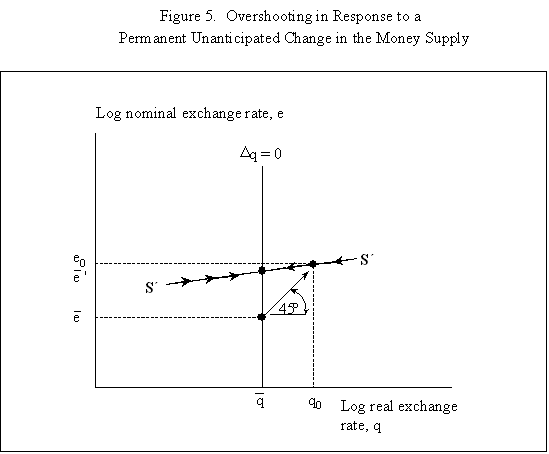
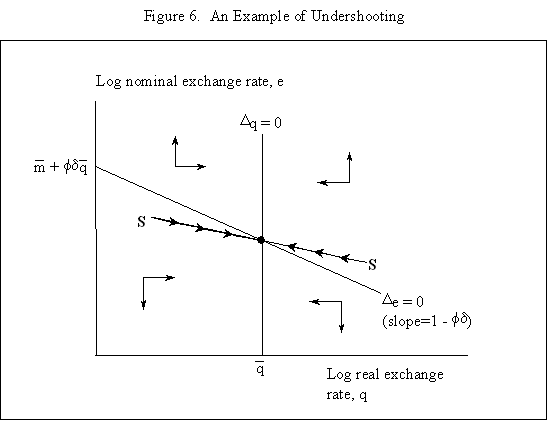
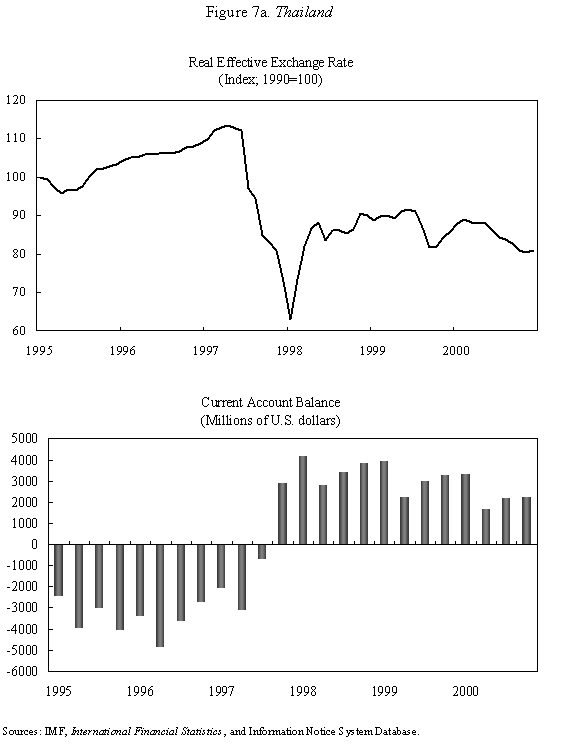
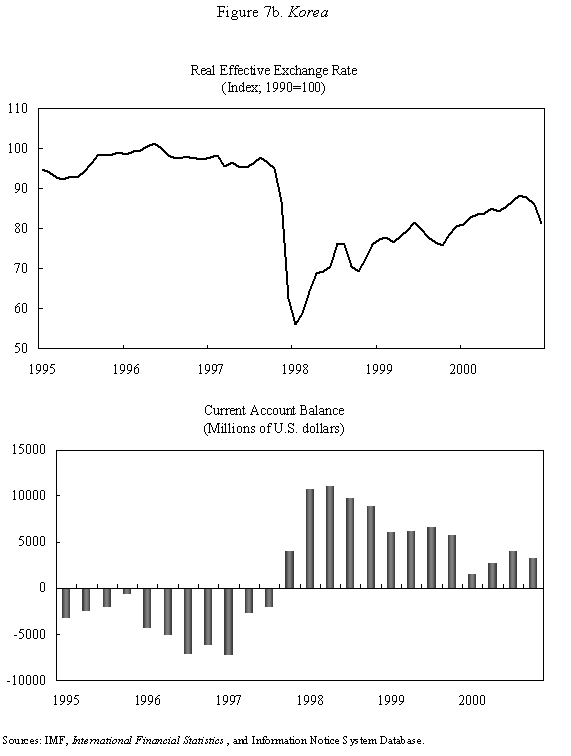
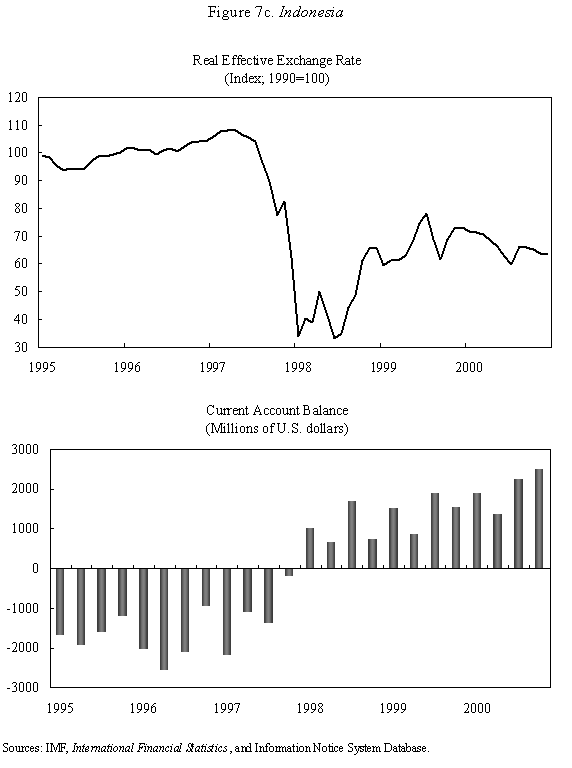
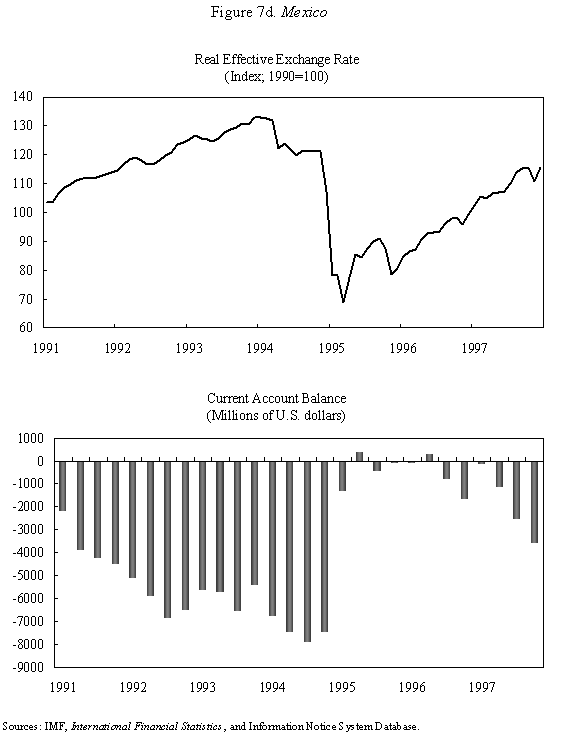
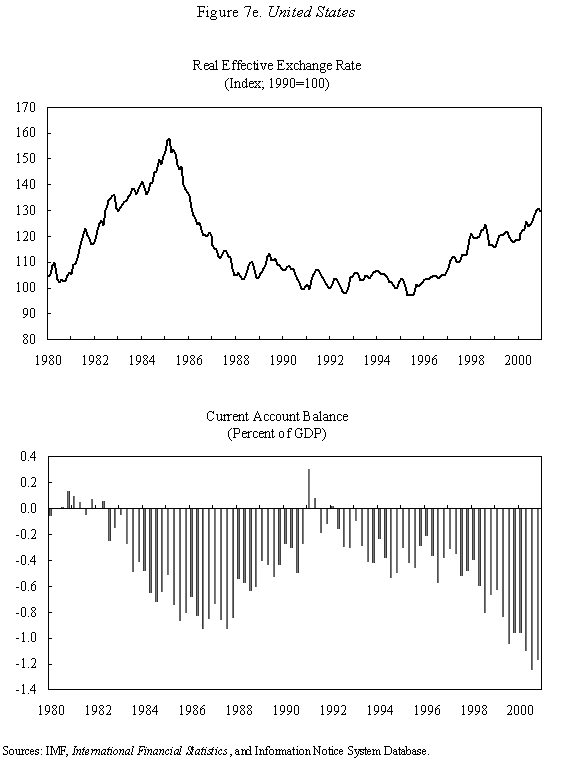
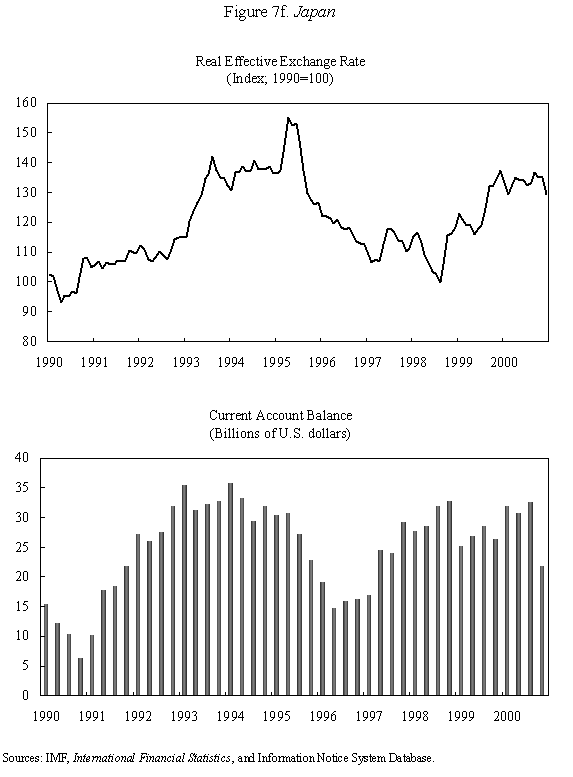
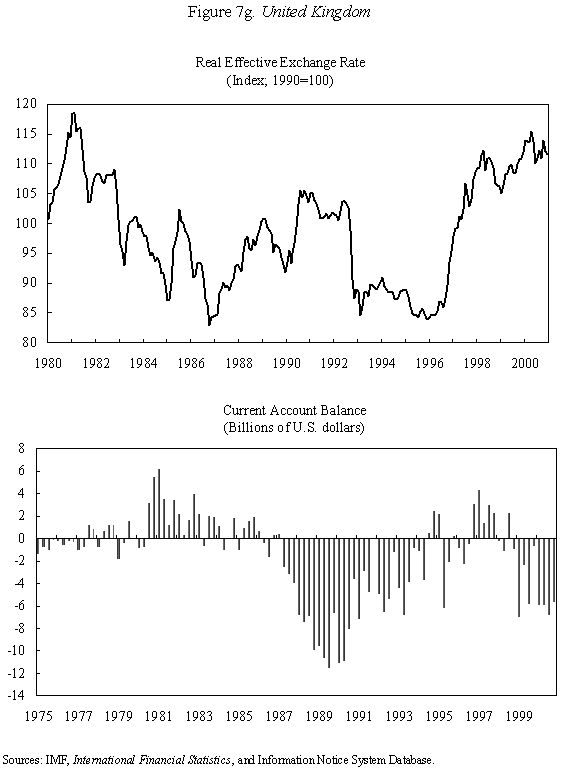
Equations (5) and (6) are graphed in Figure 4, which is drawn under the assumption that Because prices do not adjust immediately in response to shocks, the economy is not necessarily at its long-run equilibrium, given by the intersection of the two curves. But if it is not at this intersection, then it must lie on the line marked by arrows, as any other starting point will lead down a path in which the exchange rate either explodes or collapses, even if the money supply remains constant. The microfoundations needed to justify why the economy must lie on the "saddle-path" (the line with arrows) in monetary models were just beginning to be worked out at the time Dornbusch's article was being written. (The first serious attempt is Brock, 1975.) In 1977, Dornbusch could only assure us that all paths except those on the dashed line "did not make sense." That answer, of course, was not entirely satisfactory, and many of us remained fascinated by the possibility that the economy could end up on path characterized by a self-fulfilling nominal asset price bubble. Numerous people worked for many years justifying this not-so-minor assumption in the Dornbusch model (and related monetary models), using both empirical methods (e.g., Flood and Garber, 1980) and theoretical reasoning (e.g., Obstfeld and Rogoff, 1983). The short answer, it seems, is that Rudi was right, and the "saddle-path" assumption-that the economy must lie on the dashed line-is quite reasonable.19 We are now ready to graphically demonstrate the overshooting result. Recall that the mental exercise that Dornbusch considered was that of a one-time permanent change in the money supply, which in the long run (imposing the saddle-path assumption) must lead to a proportionate depreciation of both the price level and the exchange rate. But in the short run, the price level is fixed, so what happens to the exchange rate? Well, when the exchange rate jumps in response to the initial monetary surprise, q and e, the real exchange and the nominal exchange rate, have to move in proportion. (This is more or less what happens in practice as well.) Figure 5 illustrates the determination of initial post-shock exchange rate, which must lie at the intersection of the 45-degree line and the "saddle-path" line (marked by arrows). As one can see, the exchange rate must overshoot its long-run equilibrium. I have only presented a graphical depiction of overshooting, but it is not hard to fill in the algebra. For a more formal derivation, I will leave it for the reader to look at Dornbusch (1976) or the exposition in Chapter 9 in my 1996 book with Obstfeld, since it is not essential to our discussion here. What has one achieved by filling in all these algebraic details? Is there anything that was not already obvious by looking at equations (1) and (2)? First, because we can actually solve the model formally, it is possible not only to talk about overshooting from a qualitative perspective, but from a quantitative perspective. One can show what features of the model (e.g., very slow price adjustment) give rise to a high level of overshooting, and therefore a high level of exchange rate volatility. Second, one can now easily analyze a much richer menu of disturbances, such as anticipated monetary shocks, though again I will leave it for the reader to look at other references for details. Third, a formal analysis brings out subtle details such as the assumption of no speculative asset price bubbles. Last, but not least, a complete formulation of the model is necessary for empirical implementation. C. Undershooting I have already mentioned that overshooting does not have to happen in this model, depending on the parameters. Figure 4 and 5 are drawn under the assumption that We can go further with the equations, but I think this is enough algebra to illustrate the major points. I will not make any attempt to theoretically critique the model; it is clearly dated in many ways. But what is interesting is how some of its core ideas are sufficiently simple and powerful that they can be preserved in today's richer and better-motivated frameworks. Competing Models of Overshooting Dornbusch was not the first to advance the general notion of overshooting of economic variables. Arguably, one can even find the idea in Alfred Marshall's Principles of Economics, in his analysis of short versus long-run price elasticities. The clearest early statement of the concept is found in Samuelson's 1948 Foundations of Economics where he discusses the application of Le Chatelier's principle (from chemistry) to economics. Samuelson's discussion is largely abstract, but he demonstrates general conditions under which, if some variables adjust slowly, others may initially over-react. At or around the time of Dornbusch's writing, Kouri (1976) and Calvo and Rodriguez (1977) were proposing a very different notion of overshooting. The dynamics in their models are more parallel to Mundell's than to Dornbusch's, in that the slow-moving variable is national wealth, which adjusts only gradually over time through the current account. Obstfeld and Stockman (1985) discuss these models in their Handbook of International Economics chapter, and I will leave the reader to look there for further details and references. The general reaction of policy economists at the time was that these alternative models, while elegant, were far less relevant empirically than Dornbusch's variant. The fundamental empirical criticism was that they did not incorporate the essential ingredient of sticky prices. Certainly, any model that predicts that nominal domestic price volatility is of the same order of magnitude as exchange rate volatility patently contradicts the data. Also, the somewhat ad hoc Kouri and Calvo-Rodriguez models came along just as the more elegant intertemporal approach to the current account was being developed (by many scholars but not least including Obstfeld, Sachs and Calvo himself), so they were also quickly dated from a theoretical perspective, as well. Nevertheless, the general point that current account dynamics can have large medium term impacts on real exchange rates remains an important one empirically. It is perhaps no less important than the connection between monetary expansions and real exchange rates highlighted by the Dornbusch model. I sketch the idea below, though I admit my discussion glosses over a number of important details and assumptions which one can find in Frankel and Razin (1987) or in Chapter 4 of Obstfeld and Rogoff (1996). Ceteris paribus, during a period where a country is a large net importer of tradables, traded goods will be relatively abundant and the internal price of nontradables will be high. When the trade balance turns to surplus and tradables become relatively scarce, the real price of non-tradables will drop. One often sees this pattern in practice, particularly for countries that are forced to quickly reverse current account balances. Figures 7a-d, show the correlation of real exchange rate and current account imbalances in Thailand, Korea, Indonesia and Mexico in the 1990s. One wants to be cautious in inferring a structural relationship based on these casual correlations, which is driven by these countries' shifts in and out of crises. I believe, however, that a closer look at the data would support the view that the wealth channel was quite important in these instances. Figures 7e-g show the same kind of relationship for the United States, Japan and the United Kingdom, though in the case of the UK, the correlation is quite weak. Now it is possible, in principle, to integrate the two kinds of overshooting in a unified model, along the line of Obstfeld and Rogoff (1995). Thus the two views of overshooting can be viewed as complementary and not necessarily competing. In the generalized model, the Dornbusch type overshooting mechanism is the primary factor driving the short-run results (though there need not be overshooting depending on the model setup and parameters). The Kouri, Calvo-Rodriguez mechanism is central to the long run change in the real exchange rate. (Of course, the two effects interact, but I leave this discussion to another day.) IV. Conclusion Let me reiterate some of the lasting contributions of the Dornbusch model. First, it breathed new life into the Mundell-Fleming model, which in turn remained a central workhorse model for policy analysis for at least the next twenty to twenty-five years. Second, Dornbusch (1976) was the first paper in international finance to marry sticky prices with rational expectations, both central features of today's mainstream "post" Mundell-Fleming-Dornbusch model. Third, the Dornbusch model defines a high-water mark of theoretical simplicity and elegance in international finance, one which inspired a generation of students, and which still stands today as fundamental. Even today, the model in its original form remains relevant for policy analysis. Dornbusch (1976) is truly an extraordinary paper, one of the handful of most influential papers in macroeconomics generally over the past quarter century, and one of the most important papers in international economics over the entire twentieth century. It is a just thing that we celebrate it today. Long live the Dornbusch model!
References Black, Stanley, 1973, "International Money Markets and Flexible Exchange Rates," Princeton Studies in International Finance, 32, ch. 1_4. Brock, William A., 1975, "A Simple Perfect Foresight Monetary Model," Journal of Monetary Economics, Vol. 1 (2), pp. 133-50. Calvo, Guillermo and Carlos Rodriguez, 1977, "A Model of Exchange Rate Determination Under Currency Substitution and Rational Expectations," Journal of Political Economy, Vol. 85 pp. 617-625. Devereux, Michael and Charles Engel, 2001, "Exchange Rate Pass-through, Exchange Rate Volatility, and Exchange Rate Disconnect," Carnegie Rochester Series on Public Policy (forthcoming). Dornbusch, Rudiger, Stanley Fischer, and Paul Samuelson, 1977, "Comparative Advantage, Trade, and Payments in a Ricardian Model with a Continuum of Goods," American Economic Review, Vol. 67 (5), pp. 823-39. Dornbusch, Rudiger, 1976, "Expectations and Exchange Rate Dynamics," Journal of Political Economy, Vol. 84, pp. 1161-76. -, 1976b, "Exchange Rate Expectations and Monetary Policy," Journal of International Economics, Vol. 6, pp. 231-44. Fischer, Stanley, 1977, "Long-term contracts, rational expectations, and the optimal money supply rule; Journal of Political Economy, Vol. 85, pp. 191-205. Flood, Robert, 1980, "Explanations of Exchange-Rate Volatility and Other Empirical Regularities in Some Popular Models of the Foreign Exchange Market, " Carnegie-Rochester Conference Series on Public Policy, Vol. 15 (Autumn) pp. 219-49. Flood, Robert and Peter Garber, 1980, "Market Fundamentals versus Price-Level Bubbles: The First Tests," Journal of Political Economy, Vol. 88, 4, pp. 745-70. Frenkel, Jacob, and Assaf Razin, 1987, Fiscal policies and the World Economy, Cambridge: MIT Press. Frankel, Jeffrey, 1979, "On the Mark: A Theory of Floating Exchange Rates Based on Real Interest Differentials," American Economic Review Vol. 69, pp. 610-22. Friedman, Milton, 1953, "The Case for Flexible Exchange Rates," In Essays in Positive Economics, pp. 157-203. (Chicago: University of Chicago Press). Froot, Kenneth and Kenneth Rogoff, "Perspectives on PPP and Long-Run Real Exchange Rates," Handbook of International Economics, Vol. 3, Gene Grossman and Kenneth Rogoff (eds.), (Amsterdam: Elsevier Science Publishers B.V., 1995): 1647-88. NBER Working Paper 4952. Genberg, Hans and Henryk Kierzkowski, 1979, "Impact and Long-Run Effects of Economic Disturbances in a Dynamic Model of Exchange Rate Determination." Weltwirtschaftliches Archiv, Heft 4, pp. 605-28. Gray, Jo Anna, 1976, "Wage Indexation: A Macroeconomic Approach," Journal of Monetary Economics, Vol. 2 (April), RBR - I6111. Kouri, Penti, 1976, "The Exchange Rate and the Balance of Payments in the Short Run and the Long Run: A Monetary Approach," Scandinavian Journal of Economics Vol. 78, pp. 280-308. Lucas, Robert, 1973, "Some International Evidence on Output-Inflation Tradeoffs," American Economic Review, Vol. 63 (3), pp. 326-334. Meade, James, 1951, The Balance of Payments. London: Oxford University Press. Meese, Richard and Kenneth Rogoff, 1983, "Empirical Exchange Rate Models of the Seventies: Do they Fit Out Of Sample?" Journal of International Economics, 14, Mundell, Robert, 1963, "Capital Mobility and Stabilization Policy under Fixed and Flexible Exchange Rates," Canadian Journal of Economics, 29, pp. 475-485. Mussa, Michael, 1982, "A Model of Exchange Rate Dynamics," Journal of Political Economy, 90 (February), pp. 74-104. -, 1986, "Nominal exchange rate regimes and the behavior of real exchange rates: Evidence and implications," Carnegie Rochester Series on Public Policy, Vol. 25, 117-214. Obstfeld, Maurice, and Alan Stockman, 1985, "Exchange-Rate Dynamics," R. Jones and P. Kenen (eds.), Handbook of International Economics, Vol. 2. (Amsterdam: North-Holland). Obstfeld, Maurice and Kenneth Rogoff, 1983, "Speculative Hyperinflations in Maximizing Models: Can We Rule Them Out?" Journal of Political Economy, 91, (August) pp. 675-687. -, 1984, "Exchange Rate Dynamics with Sluggish Prices under Alternative Price-Adjustment Rules," International Economic Review 25 (February), pp. 159-174. -, 1995, "Exchange Rate Dynamics Redux," Journal of Political Economy, 103, -, 1995, "The Mirage of Fixed Exchange Rates," Journal of Economic Perspectives, 9, pp. 73-96. -, 1996, Foundations of International Macroeconomics (Cambridge, Massachusetts: MIT Press). -, 2000, "New Directions for Stochastic Open Economy Models," Journal of International Economics 50 (February), pp. 117-53. -, 2001, "The Six Major Puzzles in International Macroeconomics: Is there a Common Cause?" (with Maurice Obstfeld), in Ben Bernanke and Kenneth Rogoff (eds.), NBER Macroeconomics Annual 2000 (Cambridge: MIT Press). 339-390. -, 2002, "Risk and Exchange Rates," NBER Working Paper 6694 (August 1998). Forthcoming in Elhanan Helpman and Efraim Sadka, eds., Contemporary Economic Policy: Essays in Honor of Assaf Razin. (Cambridge: Cambridge University Press). Obstfeld, Maurice, 2000, "International Macroeconomics: Beyond the Mundell-Fleming Model," IMF Staff Papers, Vol. 47, Special Issue. 1st Annual Research Conference, Mundell-Fleming Lecture. Rogoff, Kenneth, 1996, "The Purchasing Power Parity Puzzle," Journal of Economic Literature 34 (June), pp. 647-68. Rogoff, Kenneth, 2001, "The Failure of Empirical Exchange Rate Models: No Longer New but Still True," Economic Policy Web Essay No.1 (October). Taylor, John and Edmund Phelps, 1977, "Stabilizing Powers of Monetary Policy Under Rational Expectations" (with E.S. Phelps), Journal of Political Economy, 84, February 1977. Reprinted in E.S. Phelps (ed.) Studies in Macroeconomic Theory: Employment and Inflation, Academic Press, 1979. Woodford, Michael, 2002, Optimizing Models with Nominal Rigidities, unpublished book manuscript, Princeton University. Woodford, Michael, and Julio J. Rotemberg, 1997, "An Optimization-Based Econometric Model for the Evaluation of Monetary Policy," NBER Macroeconomics Annual 12: 297-346. 1 Kenneth Rogoff is Economic Counsellor and Director of the Research Department at the International Monetary Fund. The author would like to acknowledge helpful comments from Maurice Obstfeld, Robert Flood, Eduardo Borensztein and Carmen Reinhart, and research assistance from Priyadarshani Joshi, Kenichiro Kashiwase and Rafael Romeu. 2 See Obstfeld and Rogoff (1995, 1996, 2000) and Brian Doyle's New Open Economy Macroeconomics homepage, http://www.geocities.com/brian_m_doyle/open.html. 3 The intertemporal approach reached its pinnacle with the publication of Jacob Frenkel and Assaf Razin's 1987 book, completed just after Frenkel's arrival as Economic Counsellor at the IMF. As I shall highlight in Section IV, the main empirical failing of the intertemporal approach is that it imposed fully flexible prices and wages, an assumption which seems patently at odds with the data. 4 When I first took Rudi's course at MIT in 1977, I had never before studied international finance. Not being socialized in the field, I found it quite odd that a depreciation of the home exchange rate should be described as a rise in e, rather than a fall which seems more natural. This is, of course, the convention in the theory of international finance, and it is one I have always felt awkward about passing on to my own students at Harvard and Princeton. It is only now, having just arrived as Economic Counsellor at the International Monetary Fund, that I have come to appreciate the wisdom of the standard convention. Already, on more than one occasion I have been involved in meetings on crisis countries in which the area department director has exclaimed "The exchange rate is completely collapsing!" and then pointed his finger upward at the ceiling. It makes me ever the more grateful for Rudi's training... 5 Equation (1) is commonplace these days, but remember that Mundell's (1963) model had i= i*, since the technology for dealing with expectations had not yet been developed at the time of his writing. 6 See especially, the interesting attempt by Devereux and Engel (2002) to reconcile their "New Open Economy Macroeconomics" paper with the data, forthcoming in a Carnegie-Rochester conference volume devoted to the topic. (See also, Obstfeld and Rogoff, 2002, who show how the risk premium can potentially be quite large in empirical exchange rate equations.) 7 The property of long-run monetary neutrality is not quite as innocuous or general as it seems. As Obstfeld and Rogoff (1995, 1996) stressed, if a monetary shock leads to current account imbalances, the ensuing wealth shifts can have long-lasting real effects far beyond the length of fixity in any nominal contracts. However, this effect turns out to be of secondary importance in this context. 8 One frame of references is a comparison with citations to the celebrated Ricardian trade model of Dornbusch, Fischer and Samuelson (1977), which has been enormously influential across a broad range of trade issues, and has become a workhorse model in the field. Dornbusch, Fischer and Samuelson (1977) had 90 citations over the period 1977-2001, only one tenth as many as Dornbusch (1976). 9 See Rogoff (2001). In their chapter for the 1994 Handbook of International Economics, Frankel and Rose observe that scores of attempts to reverse the Meese-Rogoff finding had only served to reinforce it. More recent work can be found in papers presented the September 2001 Conference on Empirical Exchange Rate Modeling, http://www.ssc.wisc.edu/~cengel/ExchangeRateConference/exrate.htm. The proceeds are to be published in the February 2003 Journal of International Economics. 10 The real interest rate is formed by taking the one-year nominal interest rate and subtracting off lagged twelve-month inflation. 11 Meese and Rogoff (1988) find that it is very difficult to detect any reliable relationship between real interest rates and real exchange rates for the major currencies. 12 Dornbusch (1976), and Friedman (1953) writing before him, clearly anticipated that under floating exchange rates, the monetary authorities would allow nominal interest rates to fluctuate in response to real and financial market shocks far more than has actually turned out to be the case. 13 See especially, Obstfeld and Rogoff (2001). 14 Stanley Black's 1973 Princeton International Finance Discussion Paper appears to have been the first international finance paper to incorporate rational expectations; it is cited in Dornbusch's article. 15 In truth, neither the Dornbusch nor the Mundell-Fleming version of the Keynesian model had a well-developed theory of how the economy should move from short to long-run equilibrium, and this important detail only came later in new open economy macroeconomics versions of the models. 16 In fact, for the kinds of shocks Dornbusch (1976) analyzed, the Mussa price adjustment equation is observationally equivalent; see Obstfeld and Rogoff (1984). Frankel (1979) offers an alternative way to extend the Dornbusch model to allow for money growth shocks, though again it turns out to be observationally equivalent to the Mussa model. 17 In general, the final term in the Mussa price adjustment mechanism has the level of inflation that would be needed to clear the goods market if it were already in equilibrium. In the simple model I present here, that rate of inflation just happens to equal the rate of exchange rate depreciation-see Obstfeld and Rogoff (1984) or (1996, Chapter 9) for the general case. 18 See Froot and Rogoff (1995) and Rogoff (1996). 19 For a more detailed discussion, see Obstfeld and Rogoff (1996), Chapter 8. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IMF EXTERNAL RELATIONS DEPARTMENT
| Public Affairs | Media Relations | |||
|---|---|---|---|---|
| E-mail: | publicaffairs@imf.org | E-mail: | media@imf.org | |
| Fax: | 202-623-6278 | Phone: | 202-623-7100 | |